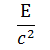|
La théorie de la relativité
(1949)
Les mathématiques traitent exclusivement des relations des concepts entre eux, sans considérer leurs relations avec l'expérience.
La physique aussi traite de concepts mathématiques ; ces concepts acquièrent cependant
un contenu physique grâce à la détermination précise de leurs relations avec les objets de l'expérience. Ceci est particulièrement
le cas des concepts de mouvement, d'espace
et de temps.
La théorie de la relativité est cette théorie physique qui est basée sur une interprétation physique cohérente
de ces trois concepts. Le nom de « théorie
de la relativité » est lié au fait que le mouvement, du point de vue de l'expérience possible,
apparaît toujours comme le mouvement relatif d'un objet par rapport à un autre (par exemple d'une voiture par rapport
au sol, de la terre par rapport au soleil et aux étoiles fixes). Jamais on n'observe un
« mouvement par rapport à l'espace », ou, comme on
dit, « un mouvement absolu ».
Le « principe de relativité » dans le sens le plus
large est contenu dans cet énoncé : la totalité des phénomènes physiques est d'un caractère
tel qu'elle ne donne aucune raison d'introduire le concept de « mouvement
absolu » ou, pour parler plus brièvement mais moins exactement :
Il n'y a pas de mouvement absolu.
Il pourrait sembler que notre connaissance a peu de profit à tirer d'un tel énoncé négatif. En réalité, il présente une forte restriction
aux lois (concevables) de la nature. Dans ce sens, il existe une analogie entre la théorie de la relativité et la thermodynamique. Cette
dernière est également basée sur un énoncé négatif :
« Il n'y a pas de mouvement perpétuel. »
Le développement de la théorie de la relativité s'est effectué en deux étapes :
« théorie de la relativité restreinte »
et « théorie de la relativité générale ».
Cette dernière suppose la validité de la première comme cas limite et est sa continuation logique.
A. — Théorie de la relativité restreinte
Interprétation physique de l'espace et du temps dans la mécanique classique.
La géométrie, du point de vue physique, est l'ensemble des lois selon lesquelles des corps rigides en repos relatif peuvent être
placés les uns par rapport aux autres (par exemple un triangle est formé de trois baguettes dont les extrémités se touchent d'une façon permanente).
Il est supposé qu'avec une telle interprétation les lois d'Euclide sont valables.
« L'espace », dans cette interprétation,
est en principe un corps rigide infini (ou charpente) auquel la position de tous les autres corps est rapportée (corps de référence).
La géométrie analytique (cartésienne) emploie comme corps de référence représentant l'espace trois baguettes rigides perpendiculaires
les unes aux autres,
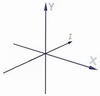 sur lesquelles les « coordonnées »
(x, y, z) des points de l'espace sont mesurées, de la façon bien connue, comme des projections perpendiculaires (à l'aide d'une unité de mesure rigide).
sur lesquelles les « coordonnées »
(x, y, z) des points de l'espace sont mesurées, de la façon bien connue, comme des projections perpendiculaires (à l'aide d'une unité de mesure rigide).
La physique traite « d'événements »
dans l'espace et le temps. À chaque événement appartient, outre ses coordonnées d'espace x, y, z,
une valeur temporelle t. Cette dernière était considérée comme mesurable par une horloge (processus périodique idéal) d'une
dimension spatiale négligeable. Cette horloge H doit être considérée comme étant au repos en un point du système de coordonnées,
par exemple à l'origine des coordonnées (z = y = z = 0).
L'instant auquel un événement à lieu au point P (x, y, z) est alors défini comme
étant le temps indiqué par l'horloge H simultanément avec l'événement. Ici, le concept
« simultané » était supposé avoir un sens physique,
sans être spécialement défini. C'est là un manque d'exactitude qui paraît bénin seulement parce que, à l'aide de la lumière
(dont la vitesse est pratiquement infinie quand on la compare aux vitesses courantes), la simultanéité d'événements distants dans
l'espace peut apparemment être déterminée immédiatement.
La théorie de la relativité restreinte fait disparaître ce manque de précision en définissant la simultanéité
physiquement au moyen de signaux lumineux. L'instant t de l'événement en P
est l'indication de l'horloge H
au moment de l'arrivée d'un signal lumineux parti de l'événement, corrigé relativement au temps dont a besoin le signal lumineux
pour parcourir la distance. La correction suppose (postule) que la vitesse de la lumière est constante.
Cette définition réduit le concept de simultanéité d'événements distants dans l'espace à celui de simultanéité
d'événements se produisant au même lieu (coïncidence), c'est-à-dire l'arrivée du signal lumineux en H et la lecture de H.
La mécanique classique est fondée sur le principe de Galilée : Un corps est en mouvement
rectiligne et uniforme tant que d'autres corps n'agissent pas sur lui. Cet énoncé ne peut pas être valable pour des systèmes de
coordonnées se mouvant arbitrairement. Sa validité ne s'étend qu'à ce qu'on appelle « systèmes
d'inertie ». Les systèmes d'inertie sont en un mouvement rectiligne et uniforme les uns par
rapport aux autres. Dans la physique classique, les lois sont valables seulement par rapport à l'ensemble des systèmes d'inertie
(principe de relativité restreinte).
On peut maintenant facilement comprendre le dilemme qui a conduit à la théorie de la relativité restreinte. L'expérience et la
théorie ont graduellement conduit à la conviction que la lumière se propage toujours dans le vide avec la même vitesse c,
indépendamment de sa couleur et de l'état de mouvement de la source lumineuse (principe de constance de la vitesse de la lumière,
que nous appellerons dans ce qui suit « principe-L »).
Maintenant, des considérations intuitives élémentaires semblent montrer que le même rayon lumineux ne peut pas se mouvoir
relativement à tous les systèmes d'inertie avec la même vitesse c. Le principe-L paraît contredire le principe de
relativité restreinte.
Il se trouve cependant que cette contradiction n'est qu'apparente, elle repose essentiellement sur le préjugé du caractère absolu du
temps, ou plutôt de la simultanéité d'événements distants. Nous venons de voir que x, y, z,
et t d'un événement peuvent, pour le moment, être définis seulement par rapport à un certain système de coordonnées choisi
(système d'inertie). La transformation des x, y, z, t d'événements, qui doit
être effectuée quand on passe d'un système d'inertie à un autre (transformation de coordonnées), est un problème qui ne peut pas être
résolu sans certaines hypothèses physiques. Toutefois, le postulat suivant est précisément suffisant pour une
solution : Le principe-L demeure vrai pour tous les systèmes d'inertie (application du
principe de relativité restreinte au principe-L). Les transformations ainsi définies, qui sont linéaires
en x, y, z, t, sont appelées transformations de Lorentz. Les transformations
de Lorentz sont, au point de vue formel, caractérisées par l'exigence que l'expression
dx2 + dy2 + dz2 - c2dt2,
qui est formée à partir des différentielles des coordonnées dx, dy, dz, dt
de deux événements infiniment proches, soit invariante (c'est-à-dire qu'au cours de la transformation elle se transforme en la même
expression formée avec les différentielles des coordonnées dans le nouveau système).
À l'aide des transformations de Lorentz, le principe de relativité restreinte peut être exprimé ainsi :
Les lois de la nature sont invariantes par rapport aux transformations de Lorentz (c'est-à-dire, une loi de la nature ne change pas
sa forme, si l'on y introduit un nouveau système d'inertie à l'aide d'une transformation de Lorentz sur x, y, z, t).
La théorie de la relativité restreinte a conduit à une claire intelligence des concepts d'espace et de temps et,
par suite, à faire connaître le comportement des règles et des horloges en mouvement. Elle a en principe éliminé le concept de simultanéité
absolue et, par là, celui d'action instantanée à distance dans le sens de
.
Elle a montré comment la loi du mouvement doit être modifiée quand il s'agit de mouvements qui ne sont pas d'une petitesse négligeable
comparés à la vitesse de la lumière. Elle a conduit à une clarification formelle des équations de Maxwell du champ
électromagnétique ; elle a, en particulier, conduit à une intelligence de l'unité essentielle
du champ électrique et du champ magnétique. Elle a réuni en une seule loi les lois de la conservation de la quantité de mouvement et
de l'énergie et démontré l'équivalence de la masse et de l'énergie. Du point de vue formel, on peut caractériser ainsi l'oeuvre accomplie
par la théorie de la relativité restreinte : elle a montré quel rôle joue la constante universelle
c (vitesse de la lumière) dans les lois de la nature et démontré qu'il y a une connexion étroite entre la forme sous laquelle
le temps, d'une part, et les coordonnées d'espace, d'autre part, entrent dans les lois de la nature.
B. — Théorie de la relativité générale
La théorie de la relativité restreinte conservait la base de la mécanique classique sur un point fondamental, c'est-à-dire
l'énoncé : Les lois de la nature sont valables seulement par rapport aux systèmes
d'inertie. Les transformations « permises »
pour les coordonnées (c'est-à-dire celles qui laissent la forme des lois inchangée) sont exclusivement les transformations
(linéaires) de Lorentz. Cette restriction est-elle réellement basée sur des faits physiques ?
L'argument suivant montre d'une façon convaincante que ce n'est pas le cas.
Principe d'équivalence. Un corps a une masse inerte (résistance à l'accélération) et une masse pesante (qui détermine le poids
d'un corps dans un champ gravifique donné, par exemple celui à la surface de la Terre). Ces deux quantités si différentes d'après
leurs définitions sont, d'après l'expérience, caractérisées par un seul et même nombre. Il doit y avoir une raison plus profonde
pour cela. Le fait peut aussi être décrit de la manière suivante : Dans un champ de
gravitation, des masses différentes subissent la même accélération. Finalement, on peut aussi l'exprimer
ainsi : Des corps dans un champ de gravitation se comportent comme en l'absence d'un
champ de gravitation si, dans le dernier cas, le système de référence employé est un système de coordonnées uniformément
accéléré (au lieu d'un système d'inertie).
Il ne paraît pas, par conséquent, y avoir de raison d'interdire l'interprétation suivante du dernier cas. On considère le système
comme étant « au repos » et le champ de gravitation
« apparent » qui existe par rapport à lui comme
« réel ». Ce champ de gravitation
« engendré » par l'accélération du système de
coordonnées serait naturellement d'une étendue illimitée, de telle sorte qu'il ne pourrait être produit par des masses graves
dans une région finie ; cependant, si nous cherchons une théorie du champ, ce fait ne
doit pas nous décourager. Par cette interprétation, le système d'inertie perd sa signification et l'on a une
« explication » de l'égalité de la masse
pesante et de la masse inerte (la même propriété de la matière apparaît comme poids ou comme inertie, selon le mode de description).
Envisagée au point de vue formel, l'admission d'un système de coordonnées, qui est accéléré par rapport aux coordonnées
« d'inertie » originelles, signifie
l'admission de transformations de coordonnées non linéaires, d'où une puissante extension de l'idée d'invariance,
c'est-à-dire du principe de relativité.
Tout d'abord, une discussion approfondie, qui se sert des résultats de la théorie de la relativité restreinte, montre
qu'avec une telle généralisation les coordonnées ne peuvent plus être interprétées directement comme des résultats de mesure.
Seules les différences de coordonnées, ainsi que les grandeurs de champ qui décrivent le champ de gravitation, déterminent
les distances mesurables entre les événements. Quand on s'est vu forcé d'admettre des transformations de coordonnées non
linéaires comme transformations entre systèmes de coordonnées équivalents, il paraît très simple d'admettre toutes les
transformations continues de coordonnées (qui forment un groupe), c'est-à-dire d'admettre des systèmes de coordonnées
curvilignes arbitraires dans lesquels les champs sont décrits par des fonctions régulières (principe de relativité générale).
Il n'est pas difficile maintenant de comprendre pourquoi le principe de relativité générale
(se basant sur le principe d'équivalence) a conduit à une théorie de la gravitation. Il existe un genre spécial d'espace, dont
nous pouvons supposer la structure physique (champ) comme connue précisément sur la base de la théorie de la relativité restreinte.
C'est l'espace vide sans champ électromagnétique et sans matière. Il est entièrement déterminé par sa propriété
« métrique ».
Soit dx0 , dy0 ,
dz0 , dt0 ,
les différences de coordonnées de deux points infiniment proches (événements), alors
(1)
ds2 = dx02 + dy02 +
dz02 - c2dt02
est une quantité mesurable, qui est indépendante du choix spécial du système d'inertie. Si l'on introduit dans cet espace
les nouvelles coordonnées x1, x2, x3, x4 par une transformation générale de coordonnées,
alors la quantité ds2 pour les mêmes deux points a une expression de la forme
(2)
ds2 =
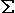 gik
dxidxk
(sommé par rapport à i et k de 1 à 4), gik
dxidxk
(sommé par rapport à i et k de 1 à 4),
où
gik
=
gki . Les gik qui forment un « tenseur
symétrique » et sont des fonctions continues de x1 ... x4 décrivent alors,
conformément au « principe d'équivalence », un champ de
gravitation d'un genre spécial (c'est-à-dire un champ qui peut de nouveau être ramené à la forme (1)). Les recherches de Riemann sur les
espaces métriques permettent d'indiquer exactement les propriétés mathématiques de ce champ gik
(« condition de Riemann »). Cependant, ce que nous
cherchons ce sont les équations qui sont satisfaites par des champs de gravitation
« généraux ». Il est naturel de supposer qu'eux aussi
peuvent être décrits comme des champs tensoriels du type gik, qui n'admettent pas généralement une transformation
en la forme (1), c'est-à-dire qui ne satisfont pas à la « condition de
Riemann », mais à des conditions plus faibles, lesquelles, exactement comme la condition de
Riemann, sont indépendantes du choix des coordonnés (c'est-à-dire, elles sont généralement invariantes). Un raisonnement formel simple
conduit à des conditions plus faibles, qui sont étroitement liées à la condition de Riemann.
Ces conditions sont les véritables équations
du champ de gravitation pur (en dehors de la matière et en l'absence de champ électromagnétique).
Ces équations font apparaître les lois de la gravitation de
comme une loi approchée et expliquent en outre certains petits effets qui ont été confirmés par l'observation (déviation de la lumière
par le champ de gravitation d'une étoile, influence du potentiel gravifique sur la fréquence de la lumière émise, lente rotation des
trajectoires elliptiques des planètes — mouvement du périhélie de Mercure). Elles fournissent de plus une explication de l'expansion
des systèmes galactiques, qui se manifeste par un déplacement vers le rouge de la lumière émise par ces systèmes.
La théorie de la relativité générale est encore incomplète en ce sens qu'il n'a été possible de l'appliquer
d'une manière satisfaisante qu'aux champs de gravitation, mais non pas au champ total. Nous ne savons pas encore avec certitude
par quel mécanisme mathématique le champ total dans l'espace doit être décrit, et quelles sont les lois générales invariantes auxquelles
ce champ total obéit. Une chose cependant paraît certaine : le principe de relativité générale
sera un instrument nécessaire et efficace pour la solution du problème du champ total.
|

![]() (Épigraphe) Relativité générale - 1919
(Épigraphe) Relativité générale - 1919
![]()
![]() Vitesse de la lumière et continuum espace-temps (1936)
Vitesse de la lumière et continuum espace-temps (1936)
![]()
![]() Qu'est-ce que la théorie de la relativité ? (1919)
Qu'est-ce que la théorie de la relativité ? (1919)
![]()
![]() La théorie de la relativité (1949)
La théorie de la relativité (1949)
![]()
![]() A. Théorie de la relativité restreinte
A. Théorie de la relativité restreinte
![]()

 sur lesquelles les «
sur lesquelles les «